Pular para o conteúdo principal
Pesquisar
Pesquisar este blog
Bendita Matemática
Páginas
Curiosidades
Geometria Hiperbólica
Mais…
Postagens
Mostrando postagens de 2009
Mostrar tudo
Visualizações de página dos últimos 30 dias
Postado por
Professor Carlos Bino
setembro 06, 2009
É fácil ganhar dinheiro do dia para noite?
Postado por
Professor Carlos Bino
setembro 02, 2009
Alunos aprovados na 1ª fase da OBMEP 2009
Postado por
Professor Carlos Bino
agosto 10, 2009
A beleza da Matemática
Postado por
Professor Carlos Bino
julho 27, 2009
Simulado do ENEM
Postado por
Professor Carlos Bino
maio 31, 2009
O romance da dança com a matemática: primeiras notações
Postado por
Professor Carlos Bino
abril 29, 2009
Dia Nacional da Matemática
Postado por
Professor Carlos Bino
março 22, 2009
Uma visão matemática na explicação do azar
Postado por
Professor Carlos Bino
março 13, 2009
Mancala
Postado por
Professor Carlos Bino
fevereiro 15, 2009
Rubik 360
Postado por
Professor Carlos Bino
fevereiro 11, 2009
Qual é a graça?
Postagens mais recentes
Postagens mais antigas
Página inicial
Mais visualizadas nos últimos 30 dias
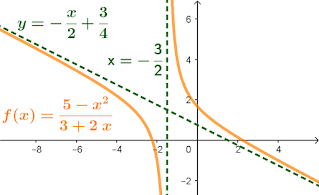
Postado por
Carlos Bino
janeiro 13, 2017
Arco triplo
Postado por
Carlos Bino
junho 29, 2017
Pontos equidistantes do centro e de algum lado de um quadrado
Postado por
Carlos Bino
março 05, 2021
Assíntota oblíqua
