Pular para o conteúdo principal
Pesquisar
Pesquisar este blog
Bendita Matemática
Páginas
Curiosidades
Geometria Hiperbólica
Mais…
Postagens
Mostrando postagens de 2010
Mostrar tudo
Visualizações de página dos últimos 30 dias
Postado por
Professor Carlos Bino
novembro 11, 2010
Choques na cabeça melhoram desempenho em matemática
Postado por
Professor Carlos Bino
outubro 24, 2010
Aplicações de Razão e Proporção
Postado por
Professor Carlos Bino
maio 08, 2010
Alguns sistemas de numeração
Postado por
Professor Carlos Bino
fevereiro 27, 2010
Uma boa maneira de calcular raízes quadradas de números quadrados perfeitos
Postado por
Professor Carlos Bino
fevereiro 21, 2010
Cálculo de feira
Postado por
Professor Carlos Bino
fevereiro 20, 2010
Falso espiral
Postado por
Professor Carlos Bino
fevereiro 15, 2010
Erros de cálculos quase quebraram o sistema financeiro mundial!
Postado por
Professor Carlos Bino
janeiro 25, 2010
Quem inventou a matemática?
Postado por
Professor Carlos Bino
janeiro 20, 2010
Um macaco primitivo aprendeu conceitos básico de matemática
Postado por
Professor Carlos Bino
janeiro 08, 2010
Quem diria!!!! Homens e Mulheres têm a mesma capacidade matemática!!!
Postagens mais recentes
Postagens mais antigas
Página inicial
Mais visualizadas nos últimos 30 dias
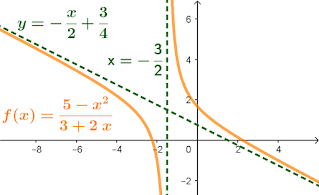
Postado por
Carlos Bino
agosto 09, 2015
Resolução de Equações do 2º grau pelo método de Viète
Postado por
Carlos Bino
março 05, 2021
Assíntota oblíqua
Postado por
Carlos Bino
janeiro 13, 2017
Arco triplo
