Postagens
Mostrando postagens de setembro, 2016
Visualizações de página dos últimos 30 dias

Postado por
Carlos Bino
Inversão de reta em relação à circunferência
- Gerar link
- Outros aplicativos
Mais visualizadas nos últimos 30 dias
Postado por
Carlos Bino
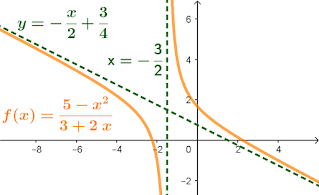
Assíntota oblíqua
- Gerar link
- Outros aplicativos
Postado por
Carlos Bino
Arco triplo
- Gerar link
- Outros aplicativos
