Pular para o conteúdo principal

Pesquisar este blog

Bendita Matemática

Bendita Matemática

Páginas

Curiosidades
Geometria Hiperbólica

Postagens

Mostrando postagens de agosto, 2015

Visualizações de página dos últimos 30 dias

Postado por Carlos Bino agosto 18, 2015

Equação da reta no plano complexo

Gerar link
Facebook
X
Pinterest
E-mail
Outros aplicativos

Postado por Carlos Bino agosto 09, 2015

Resolução de Equações do 2º grau pelo método de Viète

Gerar link
Facebook
X
Pinterest
E-mail
Outros aplicativos

Postagens mais recentes Postagens mais antigas Página inicial

Mais visualizadas nos últimos 30 dias

Postado por Carlos Bino junho 25, 2016

GEOMETRIA HIPERBÓLICA: O modelo de Disco de Poincaré

Gerar link
Facebook
X
Pinterest
E-mail
Outros aplicativos

Postar um comentário

Postado por Carlos Bino março 05, 2021

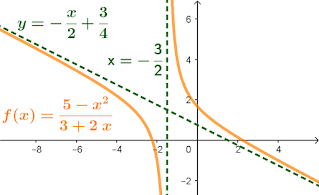
Assíntota oblíqua

Gerar link
Facebook
X
Pinterest
E-mail
Outros aplicativos

Postar um comentário

Postado por Carlos Bino abril 27, 2025

Classificação dos Sistemas Lineares: Entenda Cada Possibilidade

Gerar link
Facebook
X
Pinterest
E-mail
Outros aplicativos

Postar um comentário

Tecnologia do Blogger