Assíntota oblíqua

INTRODUÇÃO

Estava preparando uma atividade, com o auxílio do GeoGebra, quando precisei identificar as assíntotas da função

$$f(x)=\frac{5-x^2}{3+2x}$$

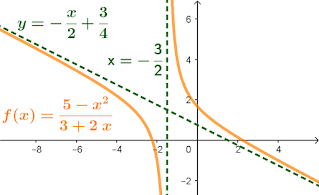Figura 1: Função $f(x)=\frac{5-x^2}{3+2x}$ com assíntotas $x=-\frac{3}{2}$ e $y=-\frac{x}{2}+\frac{3}{4}$

Identificar a assíntota vertical $x=-\frac{3}{2}$ não é uma tarefa difícil. Como a função $f$ não está definida em $x=-\frac{3}{2}$, então, verifica-se que

$$\left\{\begin{array}{l}\underset{x\rightarrow-\frac{3}{2}^-}{\lim} f(x) =-\infty \\ \underset{x\rightarrow-\frac{3}{2}^+}{\lim} f(x) =\infty \end{array}\right.$$

Porém, $f(x)\rightarrow -\infty$ quando $x\rightarrow \infty$ e $f(x)\rightarrow \infty$ quando $x\rightarrow -\infty$. Assim, não há assíntotas horizontais, porém, o GeoGebra indica que há uma assíntota oblíqua $y=-\frac{x}{2}+\frac{3}{4}$. Vamos verificar se há pontos em comum entre a curva $f$ e a reta que o software indica como assíntota oblíqua.

$$\frac{5-x^2}{3+2x}=-\frac{x}{2}+\frac{3}{4}\Rightarrow 4\cdot (5-x^2) = (3+2x)\cdot (-2x+3)\Rightarrow 20-4x^2=9-4x^2\Rightarrow 20=9$$

Desta forma, verificamos que a solução é vazia, assim, não há pontos em comum entre a reta $y=-\frac{x}{2}+\frac{3}{4}$ e a curva $f$. Logo, na Figura 2, região azul não contém pontos da curva $f$.

Figura 2: A curva $f$ não possui pontos na região azul

Sabemos que é possível que uma curva tenha pontos em comum com suas assíntotas, por isso, se a curva $f$ e a reta $y$ tivessem pontos em comum não poderíamos negar que a reta é uma das assíntotas da curva. Além disso, o fato de não terem pontos em comum, também não confirma que $y$ é uma assíntota da curva. 

Figura 3: A reta $\overline{PQ}$ não intercepta a curva $f$

Por exemplo, na Figura 3, o ponto $P$ pertence a interseção entre as assíntotas e $Q$ é um ponto da região que a curva $f$ não passa. Assim, a reta $\overline{PQ}$ não intercepta a curva $f$, mas também não é uma das assíntota.

DEFINIÇÃO DE ASSÍNTOTA

Dos livros de Cálculo Diferencial e Integral temos a noção de assíntotas verticais e horizontais que são retas cujas curvas se aproximam quando aproximamos $x$ de um número para o qual a função não está definida (no caso de assíntotas verticais) ou quando $x$ tende ao infinito positivo ou negativo (caso das assíntotas horizontais). Vamos observar o gráfico da função $g(x)=\dfrac{e^{x-1}+1}{e^{x-1}-1}$

Figura 4: função $g(x)=\dfrac{e^{x-1}+1}{e^{x-1}-1}$ e suas assíntotas

Veja que quando nos distanciamos da origem pela da função $g$ (seja por $x\rightarrow\infty, x\rightarrow-\infty$ ou $x\rightarrow 1$) , o gráfico se aproxima de uma das assíntotas. Desta forma, ao se afastar da origem, a distância entre a função $g$ e sua assíntota mais próxima tende a zero. 

$$\begin{array}{lll}\text{Distância entre }g(x) \text{ e a assintota }a:y=-1: & |g(x)-(-1)|\rightarrow 0, & \text{quando }x\rightarrow -\infty\\\text{Distância entre }g(x) \text{ e a assintota }b:x=1: & |x-1|\rightarrow 0, & \text{quando }x\rightarrow 1\\ \text{Distância entre }g(x) \text{ e a assintota }c:y=1: & |g(x)-1|\rightarrow 0, & \text{quando }x\rightarrow\infty\end{array}$$.

Vamos voltar para função $f(x)=\dfrac{5-x^2}{3+2x}$ que tem assíntota vertical $x=-\dfrac{3}{2}$ e o GeoGebra indica como assíntota oblíqua $y=-\frac{x}{2}+\frac{3}{4}$ (ver Figura 1).

Podemos facilmente verificar que a distância entre a função $f$ e a reta $x=-\dfrac{3}{2}$ $$\left|x-\left(-\dfrac{3}{2}\right)\right|\rightarrow 0$$ quando $x\rightarrow -\dfrac{3}{2}$.

Para verificar se a distância entre a função $f(x)$ e a reta $y=-\frac{x}{2}+\frac{3}{4}$ tende a 0, vamos considerar pontos genéricos de cada um com mesma abscissa

$$(x, f(x)), (x, y) \Leftrightarrow\left(x, \dfrac{5-x^2}{3+2x}\right), \left(x, -\frac{x}{2}+\frac{3}{4}\right)$$

Assim, a distância $d$ entre os pontos genéricos é

$$d=\sqrt{(x-x)^2 + (f(x)-y)^2}=\sqrt{\left(\dfrac{5-x^2}{3+2x}--\frac{x}{2}+\frac{3}{4}\right)^2}=\left|\frac{11}{8x + 12}\right|\rightarrow 0,\text{ quando } x\rightarrow\pm\infty$$

Vamos considerar a definição a seguir de assíntota de uma função.

DEFINIÇÃO 1: A reta $r$ é chamada de assíntota da função $f$ se a distância $d$ entre $r$ e $f$ tender a 0 quando $x\rightarrow\infty, x\rightarrow-\infty$ ou $x\rightarrow a$, quando $f$ não é contínua $a\in\mathbb{R}$. Chamamos $r$ de

• assíntota vertical se $r:x=a$;
• assíntota horizontal se $r:y=b$, para $b\in\mathbb{R}$;
• e assíntota oblíqua se $r:mx+q$, para $m,q\in\mathbb{R}$.

Pela Definição 1, a reta $y=-\dfrac{x}{2}+\dfrac{3}{4}$ é assíntota oblíqua da função $f(x)=\dfrac{5-x^2}{3+2x}$.

Agora que apresentamos uma definição para assíntotas, vamos mostrar uma forma de identificar as assíntotas de uma função, se existir.

EXISTÊNCIA DE ASSÍNTOTA OBLÍQUA

Vamos considerar uma função $f(x)$ com assíntota $r$. Nos livros de Cálculo Diferencial e Integral é mostrado as formas de encontrar as assíntotas verticais e horizontais, se existirem, de uma função. A saber:

• Se $f$ não está definida no número $a\in\mathbb{R}$ e $\underset{x\rightarrow a}{\lim} f(x)=\pm\infty$ então a reta $x=a$ é assíntota vertical de $f$;
• Se $\underset{x\rightarrow-\infty}{\lim}f(x)=a$ ou $\underset{x\rightarrow\infty}{\lim}f(x)=a$ então $y=a$ é assíntota horizontal de $f$.

Vamos tomar $r:y=mx+q$, desta forma, vamos considerar pontos genéricos de $f$ e $r$, respectivamente, com mesma abscissa

$$(x, f(x)), (x, y)\Leftrightarrow (x, f(x)), (x, mx+q)$$

Assim, a distância $d$ entre $f$ e $r$ é

$$d=\sqrt{(x-x)^2+[f(x)-(mx+q)]^2}=|f(x)-(mx+q)|$$

Para $x\rightarrow a$, temos

$$\lim_{x\rightarrow a} d=\lim_{x\rightarrow a}|f(x)-(mx+q)|=|\lim_{x\rightarrow a}f(x) - (m\cdot a+q)|$$

Se $f(x)$ for contínua em $a$, então $\underset{x\rightarrow a}{\lim}f(x)=f(a)=k$, assim

$$\lim_{x\rightarrow a} d=|k-(m\cdot a+q)|=C\geq 0$$

$C=0$ caso $f$ e $r$ tenha ponto em comum em $x=a$.

Se $f(x)$ não é contínua em $a$ e $\underset{x\rightarrow a}{\lim}f(x)=\pm\infty$, temos

$$\lim_{x\rightarrow a} d=|\lim_{x\rightarrow a}f(x) - (m\cdot a+q)|=\infty$$

Assim, provamos que se $\underset{x\rightarrow a}{\lim}f(x)=\pm\infty$ então $f(x)$ se aproxima de uma reta vertical $x=a$. Desta forma, a assíntota só pode ser oblíqua se 

$$\lim_{x\rightarrow-\infty}d=0\text{ ou }\lim_{x\rightarrow\infty}d=0$$

Se $\underset{x\rightarrow\infty}{\lim}f(x)=k$ para $$\underset{x\rightarrow\infty}{\lim}d=0\Rightarrow\underset{x\rightarrow\infty}{\lim}(mx+q)=k\Rightarrow m=0, q=k$$ ou seja, a assíntota é horizontal quando $\underset{x\rightarrow\infty}{\lim}f(x)=k$. De forma análoga, podemos mostrar que a assíntota também é horizontal quando $\underset{x\rightarrow-\infty}{\lim}f(x)=k$.

Assim, para existir assíntota oblíqua é necessário que $f(x)\rightarrow-\infty$ ou $f(x)\rightarrow\infty$ e a distância $d$ entre $f$ e $r$ deve tender à 0 quando $x\rightarrow-\infty$ ou $x\rightarrow\infty$.

TEOREMA 1: Uma reta $r:y=mx+q$, com $m\neq 0$, é assíntota oblíqua da função $f(x)$ se, ao menos, um dos limites a seguir existir

$$\begin{array}{ccc}
\lim_{x\rightarrow-\infty}|f(x)-(mx+q)|=0 &\text{ou}& \lim_{x\rightarrow\infty}|f(x)-(mx+q)|=0
\end{array}$$

Sem perda de generalidade, vamos tomar

$$\lim_{x\rightarrow\infty}|f(x)-(mx+q)|=0\Rightarrow \lim_{x\rightarrow\infty}(f(x)-mx)-q=0\Rightarrow q=\lim_{x\rightarrow\infty}(f(x)-mx)$$

Desta forma, pra saber o valor de $q$ precisamos conhecer o valor de $m$. Assim:

$$\lim_{x\rightarrow\infty}|f(x)-(mx+q)|=0\Rightarrow\lim_{x\rightarrow\infty}\left[\frac{f(x)}{x}-m-\frac{q}{x}\right]=0\Rightarrow m=\lim_{x\rightarrow\infty}\left[\frac{f(x)}{x}-\frac{q}{x}\right]$$

Como $\forall q$ temo $\underset{x\rightarrow\infty}{\lim}\dfrac{q}{x}=0$, então

$$m=\lim_{x\rightarrow\infty}\frac{f(x)}{x}$$

Assim, se $|m|=\infty$, então não há assíntota quando $x\rightarrow\pm\infty$, se $m=0$, então a assíntota é horizontal e se $m\in\mathbb{R}^*$ então a assíntota é oblíqua.

EXEMPLO

1) Vamos determinar a assíntota oblíqua da primeira função: $f(x)=\dfrac{5-x^2}{3+2x}$

$$m=\lim_{x\rightarrow\infty}\frac{f(x)}{x}=\lim_{x\rightarrow\infty}\frac{\frac{5-x^2}{3+2x}}{x}=\lim_{x\rightarrow\infty}\frac{5-x^2}{3x+2x^2}=-\frac{1}{2}$$

$$q=\lim_{x\rightarrow\infty}(f(x)-mx)=\lim_{x\rightarrow\infty}\left(\frac{5-x^2}{3+2x}+\frac{1}{2}x\right)=\lim_{x\rightarrow\infty}\frac{2\cdot(5-x^2)+(3x+2x^2)}{2\cdot(3+2x)}=\lim_{x\rightarrow\infty}\frac{10+3x}{6+4x}\Rightarrow q=\frac{3}{4}$$

Você verá também que $\lim_{x\rightarrow-\infty}\dfrac{f(x)}{x}=-\dfrac{1}{2}$ e $\lim_{x\rightarrow-\infty}(f(x)-mx)=\dfrac{3}{4}$

Desta forma, mostramo que a função $f(x)$ tem assíntota oblíqua $y=-\dfrac{x}{2}+\dfrac{3}{4}$, conforme indicado pelo GeoGebra.