Pular para o conteúdo principal

Pesquisar este blog

Bendita Matemática

Bendita Matemática

Páginas

Curiosidades
Geometria Hiperbólica

Postagens

Mostrando postagens de janeiro, 2017

Visualizações de página dos últimos 30 dias

Postado por Carlos Bino janeiro 28, 2017

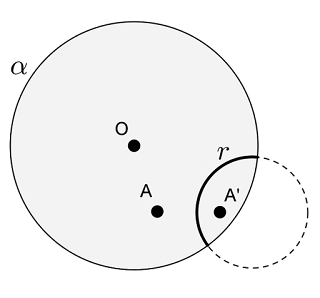
GEOMETRIA HIPERBÓLICA: H-eixo de simetria no Disco de Poincaré

Gerar link
Facebook
X
Pinterest
E-mail
Outros aplicativos

Postar um comentário

Postado por Carlos Bino janeiro 24, 2017

GEOMETRIA HIPERBÓLICA: Isometria no Disco de Poincaré - Reflexão em torno de uma h-reta

Gerar link
Facebook
X
Pinterest
E-mail
Outros aplicativos

Postar um comentário

Postado por Carlos Bino janeiro 13, 2017

Arco triplo

Gerar link
Facebook
X
Pinterest
E-mail
Outros aplicativos

Postar um comentário

Postado por Carlos Bino janeiro 08, 2017

Centro do inverso de uma circunferência que não passa pelo centro de inversão

Gerar link
Facebook
X
Pinterest
E-mail
Outros aplicativos

Postar um comentário

Postagens mais recentes Postagens mais antigas Página inicial

Mais visualizadas nos últimos 30 dias

Postado por Carlos Bino abril 27, 2025

Classificação dos Sistemas Lineares: Entenda Cada Possibilidade

Gerar link
Facebook
X
Pinterest
E-mail
Outros aplicativos

Postar um comentário

Postado por Carlos Bino julho 29, 2016

GEOMETRIA HIPERBÓLICA: Construção de h-reta

Gerar link
Facebook
X
Pinterest
E-mail
Outros aplicativos

Postar um comentário

Postado por Carlos Bino janeiro 13, 2017

Arco triplo

Gerar link
Facebook
X
Pinterest
E-mail
Outros aplicativos

Postar um comentário

Tecnologia do Blogger