jjjjjjjjjjjjjjjjjjj

Nesta postagem conheceremos uma transformação no plano hiperbólico, reflexão em torno de uma h-reta, e provaremos que esta transformação é uma isometria.

Para o bom entendimento desta publicação, é importante que tenha conhecimento sobre o modelo de Disco proposto por Poincaré, para isso sugerismo a leitura da publicação Disco de Poincaré: ponto, reta e plano. Desta forma, o plano hiperbólico $\mathbb{H}$ será a região delimitada por uma circunferência $\alpha$, com centro num ponto $O$ e raio não-nulo. Também sugerimos a leitura da publicação Métrica no Disco de Poincaré para melhor conhecimento sobre a forma de medir a distância entre dois h-pontos no Disco de Poincaré.

Para boa compreensão das demonstrações, é necessário que o leitor tenha conhecimento sobre inversão na circunferência, caso não tenha, sugerimos a leitura das publicações (nesta ordem) Inversão na circunferência, Inversão de ponto interno à circunferência $\alpha$, Inversão de ponto externo a circunferência$\alpha$, Inversão de um ponto qualquer do plano euclidiano em relação a uma circunferência, Circunferências ortogonais, Inversão de reta em relação à circunferência, Inversão de circunferência em relação a outra circunferência, Inversão de ângulos formados por retas e circunferências e Centro do inverso de uma circunferência que não passa pelo centro de inversão.

Para saber como construir h-retas, leia a publicação Construção de h-reta e H-retas perpendiculares.

jjjjjjjjjjjjjjjjjjj

Vamos definir isometria no plano $\mathbb{H}$, a definição a seguir encontrei no livro Isometria de Elon Lages Lima que foi adaptada para o plano hiperbólico.

Definição 1 - Seja uma aplicação $T:\mathbb{H}\rightarrow\mathbb{H}$, diremos que $T$ é uma isometria se:

1. $T$ é uma função biunívoca;
2. Para todo $A,B\in\mathbb{H}$ temos que $d_h(A,B)=d_h(T(A),T(B))$;
3. $T$ é uma aplicação conforme.

Vamos definir reflexão em torno de uma h-reta, considerando que no Disco de Poincaré foram definidas dois tipos de h-retas (clique aqui para ver os tipos de h-retas).

Definição 2 - Chamaremos de reflexão em torno de uma h-reta $r$ a função $\mathfrak{R}:\mathbb{H}\rightarrow\mathbb{H}$ definida como: para todo $A\in\mathbb{H}$, o reflexo de $A$ em relação a h-reta $r$ será o ponto $A'$, denotaremos por $\mathfrak{R}_r(A)=A'$, considerando a regra:

1. se $O\notin r$, então, no plano $\mathbb{E}_\infty$, $A$ é o inverso de $A'$ em relação à circunferência que gera $r$, ver Figura 1;
2. se $O\in r$, então, no plano $\mathbb{E}_\infty$, $A$ é reflexo de $A'$ em relação à reta que gera $r$, ver Figura 2.

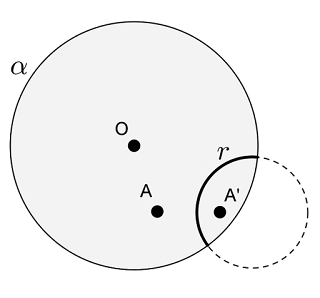Figura 1: Reflexão do $A$ em relação à
h-reta $r$ que não passa por $O$

Figura 2: Reflexão do $A$ em relação à
h-reta $r$ que passa por $O$

Diremos que $A$ e $A'$ são simétricos em relação à $r$ e $r$ será chamada de h-eixo de simetria.

Lema 1 - A reflexão em torno de uma h-reta transforma h-reta em h-reta.

DEMONSTRAÇÃO
Sejam $r$ e $s$ h-retas, sendo a primeira um h-eixo de simetria.

Se $O\in r$, então, a reflexão em torno da h-reta $r$ é igual à reflexão em torno da reta que gera $r$, denominada $\theta_r$. No plano $\mathbb{E}_\infty$, a reflexão em torno de uma reta é uma isometria, quer dizer que satisfaz condições da Definição 1 (função biunívoca e conserva distância e ângulo), considerando que a métrica do plano euclidiano, além disso, a reflexão em torno de uma reta transforma retas em retas e circunferências em circunferência. Como $\theta_r$ passa no ponto $O$, então, divide $\alpha$ em dois semicírculos, um simétrico ao outro em relação à $\theta_r$.

Figura 3: Reta $\theta_r$ divide $\alpha$ em dois semicírculos, $\alpha_1$ e $\alpha_2$, que são simétricos em relação a $\theta_r$

Se $O\in s$, então, $s$ é gerada por uma reta, denominaremos de $\theta_s$. Assim, o simétrico de $\theta_s$, em $\mathbb{E}_\infty$ é uma reta, $\theta_{s'}$, que também passa por $O$, então, o simétrico de $s$, $s'$, será um diâmetro de $\alpha$. Portanto, $s'$ é uma h-reta.

Figura 4: Reflexão da h-reta $s$ em torno da h-reta $r$ onde $O\in r,s$

Se $O\notin s$, então $s$ é gerada por uma circunferência, denominada $\beta_s$, ortogonal a $\alpha$. O simétrico de $\beta_s$ é outra circunferência, $\beta_{s'}$, também ortogonal a $\alpha$, neste caso, no plano $\mathbb{E}_\infty$, o simétrico do arco $s$, $s'$, é um arco de circunferência ortogonal a $\alpha$. Portanto, no plano $\mathbb{H}$, $s'$ é uma h-reta, ver Figura 5.

Figura 5: Reflexão da h-reta $s$ em torno da h-reta $r$ onde $O\in r$ e $O\notin s$ 

Vamos considerar que $O\notin r$, então, $r$ é uma h-reta gerada por um circunferência, que denominaremos de $\beta_r$, ortogonal a $\alpha$, ver Figura 6. Assim, $\beta_r$ divide o círculo $\alpha$ em duas regiões, uma inversa a outra em relação à $\beta_r$.

Figura 6: Circunferência $\beta_r$ divide $\alpha$ em duas regiões, $\alpha_a$ e $\alpha_b$, uma inversa a outra em relação a $\beta_r$

Sendo $s$ uma h-reta que passa por $O$, gerada pela reta $\theta_s$, e seja $O_r$ o centro da circunferência $\beta_r$, ver Figura 7. Se $\theta_s$ passa por $O_r$, então, o inverso de $\theta_s$ em relação a $\beta_r$ é a própria reta $\theta_s$ (ver Inversão de reta em relação à circunferência), veremos que o simétrico da h-reta $s$ em relação ao h-eixo simétrico $r$ é a própria h-reta $s$, ou seja, $\mathfrak{R}_r(s)=s$.

Figura 7: Reflexão de $s$ em torno de $r$ é a própria h-reta $s$

Se $O_r\notin\theta_s$, ver Figura 8, então, o inverso da reta $\theta_s$ em relação à circunferência $\beta_r$ será uma circunferência (ver Inversão de circunferência em relação a outra circunferência), denominada $\theta_{s'}$, que passa por $O_r$ e é ortogonal à circunferência $\alpha$ (ver Lema 2 - Circunferências ortogonais e Inversão de ângulos formados por retas e circunferências). Assim, o simétrico da h-reta $s$ em relação ao h-eixo de simétria $r$ é uma h-reta $s'$

Figura 8: $\mathfrak{R}_r(s)=s'$

Como a inversão é uma aplicação biunívoca, então a reflexão da h-reta $s'$, gerada pela circunferência $\theta_{s'}$ que passa por $O_r$, em torno da h-reta $r$ é a h-reta $s$ que passa por $O$.

Seja $\beta_s$ uma circunferência que não passa por $O_r$ e gera a h-reta $s$. O inverso da $\beta_s$ em relação a $\beta_r$ é outra circunferência, $\beta_{s'}$, que não passa por $O_r$ e é ortogonal a $\alpha$, ver Figura 9. Assim, a reflexão da h-reta $s$ em torno da h-reta $r$ será outra h-reta, $s'$, que não passa por $O$.

Figura 9: Reflexão da h-reta $s$ que não passa por $O$ gera pela circunferência $\beta_s$ que não passa por $O_r$

$\square$

Desta forma, mostramos que a reflexão em torno de uma h-reta transforma h-reta em h-reta. A seguir, veremos as proposições 1 e 2 que garantem que a reflexão em torno de uma h-reta satisfazem a Definição 1(a) e Definição 1(b), respectivamente.

Proposição 1 - A reflexão em torno de uma h-reta é uma função biunívoca.

DEMONSTRAÇÃO

Considerando o plano $\mathbb{E}_\infty$, tanto a inversão em relação à circunferência quanto a reflexão em torno de uma reta são aplicações biunívocas, por esta razão, a reflexão em torno de uma h-reta também é uma aplicação biunívoca.

$\square$

Proposição 2 - Sejam $A,A',B,B'\in\mathbb{H}$ e $r$ uma h-reta tais que $A'=\mathfrak{R}_r(A)$ e $B'=\mathfrak{R}_r(B)$. Então, $d_h(A,B)=d_h(A',B')$.

DEMONSTRAÇÃO

Inicialmente, se considerarmos que $A,B\in r$, para quaisquer das situações da Definição 2, teremos $A'=A$ e $B'=B$, desta forma,  $d_h(A,B)=d_h(A',B')$.  Assim, vamos considerar que ou $A\notin r$ ou $B\notin r$.

Sendo $O\in r$, ver a Figura 10, $Z_1$ e $Z_2$ são pontos ideais da h-reta determinada por $A$ e $B$, $\overline{AB}_h$, e $Z_3$ e $Z_4$ são pontos ideais da h-reta determinada por $A'$ e $B'$, $\overline{AB}_h$. Assim, teremos

$$\begin{equation}\label{equ1}


\left\{\begin{matrix}


d_h(A,B)=\left|\ln\dfrac{\overline{AZ_1}\cdot\overline{BZ_2}}{\overline{AZ_2}\cdot\overline{BZ_1}}\right|\\ \\


d_h(A',B')=\left|\ln\dfrac{\overline{A'Z_4}\cdot\overline{B'Z_3}}{\overline{A'Z_3}\cdot\overline{B'Z_4}}\right|


\end{matrix}\right.


\end{equation}$$

Como $A'$ e $B'$ são simétricos, respectivamente, a $A$ e a $B$, então a h-reta $\overline{A'B'}_h$ é simétrica à $\overline{AB}_h$, então, os pontos ideais $Z_1$ e $Z_2$ são simétricos, respectivamente, aos pontos ideais $Z_4$ e $Z_3$, assim, no plano $\mathbb{E}_\infty$, $\overline{AZ_1}\cong\overline{A'Z_4},\overline{AZ_2}\cong\overline{A'Z_3},\overline{BZ_1}\cong\overline{B'Z_4},\overline{BZ_2}\cong\overline{B'Z_3}$, assim:

$$\begin{equation}\label{equ2}


\dfrac{\overline{AZ_1}\cdot\overline{BZ_2}}{\overline{AZ_2}\cdot\overline{BZ_1}}=\dfrac{\overline{A'Z_4}\cdot\overline{B'Z_3}}{\overline{A'Z_3}\cdot\overline{B'Z_4}}\Rightarrow \ln\dfrac{\overline{AZ_1}\cdot\overline{BZ_2}}{\overline{AZ_2}\cdot\overline{BZ_1}}=\ln\dfrac{\overline{A'Z_4}\cdot\overline{B'Z_3}}{\overline{A'Z_3}\cdot\overline{B'Z_4}}\Rightarrow d_h(A,B)=d_h(A',B')


\end{equation}$$

Essa demonstração também vale para quando $O\in\overline{AB}_h$.

Figura 10: $A'=\mathfrak{R}_r(A)$ e $B'=\mathfrak{R}_r(B)$ e $d_h(A,B)=d_h(A',B')$

Se $O\notin r$, ver Figura 11, a circunferência $\beta_r$ gera a h-reta $r$; $Z_1$ e $Z_2$ são pontos ideais da h-reta $\overline{AB}_h$, determinada pelos h-pontos $A$ e $B$. Os h-pontos $A'$ e $B'$ que são simétricos, respectivamente, a $A$ e a $B$, determinam a h-reta $\overline{A'B'}_h$ que tem pontos ideais $Z'_1$ e $Z'_2$. Assim, como, no plano $\mathbb{H}$, dois h-pontos determinam uma única h-reta e sendo $A'=\mathfrak{R}_r(A)$ e $B'=\mathfrak{R}_r(B)$, temos que $\overline{A'B'}_h$  e $\overline{AB}_h$ são simétricos em relação a h-reta $r$, então, $Z'_1$ e $Z'_2$ são simétricos, respectivamente, a $Z_1$ e $Z_2$ em relação a $r$. 

Figura 11: O h-eixo de simetria não passa pelo h-ponto $O$

Considerando o plano $\mathbb{E}_\infty$ e tomando $\beta_r$ como circunferência de inversão, os pontos $A$ e $Z_2$ são inversos, respectivamente, aos pontos $A'$ e $Z'_2$, assim, da Definição 1 - Inversão na circunferência (definição de ponto inverso), temos

$$\begin{equation}\label{equ3}


\overline{O_rA}\cdot\overline{O_rA'}=\overline{O_rZ_2}\cdot\overline{O_rZ'_2}\Rightarrow\dfrac{\overline{O_rA}}{\overline{O_rZ_2}}=\dfrac{\overline{O_rZ'_2}}{\overline{O_rA'}}


\end{equation}$$

Então, o triângulo $\triangle_{AO_rZ_2}$ é semelhante ao triângulo $\triangle_{Z'_2O_rA'}$. De forma análoga, podemos demonstrar que o triângulo $\triangle_{AO_rZ_1}$ é semelhante ao triângulo $\triangle_{Z'_1O_rA'}$, ver Figura 12.

Figura 12: $\left(\triangle_{AO_rZ_2},\triangle_{Z'_2O_rA'}\right)$ e  $\left(\triangle_{AO_rZ_1},\triangle_{Z'_1O_rA'}\right)$ são pares de triângulos semelhantes

Da relação entre os triângulos $\triangle_{AO_rZ_2}$ e $\triangle_{Z'_2O_rA'}$, temos

$$\begin{equation}\label{eq2}\dfrac{\overline{AZ_2}}{\overline{A'Z'_2}}=\dfrac{\overline{O_rA}}{\overline{O_rZ'_2}}\Rightarrow\overline{O_rA}=\dfrac{\overline{AZ_2}\cdot\overline{O_rZ'_2}}{\overline{A'Z'_2}}\end{equation}$$

Da relação entre os triângulos $\triangle_{AO_rZ_1}$ e $\triangle_{Z'_1O_rA'}$, temos

$$\begin{equation}\label{eq1}\dfrac{\overline{AZ_1}}{\overline{A'Z'_1}}=\dfrac{\overline{O_rA}}{\overline{O_rZ'_1}}\Rightarrow\overline{O_rA}=\dfrac{\overline{AZ_1}\cdot\overline{O_rZ'_1}}{\overline{A'Z'_1}}\end{equation}$$

Da relação entre $\eqref{eq2}$ e $\eqref{eq1}$ temos

$$\begin{equation}\label{eq3}\dfrac{\overline{AZ_2}\cdot\overline{O_rZ'_2}}{\overline{A'Z'_2}}=\dfrac{\overline{AZ_1}\cdot\overline{O_rZ'_1}}{\overline{A'Z'_1}}\Rightarrow\dfrac{\overline{AZ_2}\cdot\overline{A'Z'_1}}{\overline{AZ_1}\cdot\overline{A'Z'_2}}=\dfrac{\overline{O_rZ'_1}}{\overline{O_rZ'_2}}\end{equation}$$

Analogamente, podemos mostrar que o triângulo $\triangle_{BO_rZ_2}$ é semelhante ao triângulo $\triangle_{Z'_2O_rB'}$ e o triângulo $\triangle_{AO_rZ_1}$ é semelhante ao triângulo $\triangle_{Z'_1O_rA'}$, ver Figura 13.

Figura 13: $\left(\triangle_{BO_rZ_2},\triangle_{Z'_2O_rB'}\right)$ e  $\left(\triangle_{BO_rZ_1},\triangle_{Z'_1O_rB'}\right)$ são pares de triângulos semelhantes

Assim, podemos encontrar

$$\begin{equation}\label{eq4}\dfrac{\overline{BZ_2}\cdot\overline{B'Z'_1}}{\overline{BZ_1}\cdot\overline{B'Z'_2}}=\dfrac{\overline{O_rZ'_1}}{\overline{O_rZ'_2}}\end{equation}$$

De $\eqref{eq3} e $\eqref{eq4}$ teremos

$$\dfrac{\overline{AZ_2}\cdot\overline{A'Z'_1}}{\overline{AZ_1}\cdot\overline{A'Z'_2}}=\dfrac{\overline{BZ_2}\cdot\overline{B'Z'_1}}{\overline{BZ_1}\cdot\overline{B'Z'_2}}\Rightarrow\dfrac{\overline{A'Z'_1}\cdot\overline{B'Z'_2}}{\overline{A'Z'_2}\cdot\overline{B'Z'_1}}=\dfrac{\overline{AZ_1}\cdot\overline{BZ_2}}{\overline{AZ_2}\cdot\overline{BZ_1}}\Rightarrow\left|\ln\dfrac{\overline{A'Z'_1}\cdot\overline{B'Z'_2}}{\overline{A'Z'_2}\cdot\overline{B'Z'_1}}\right|=\left|\ln\dfrac{\overline{AZ_1}\cdot\overline{BZ_2}}{\overline{AZ_2}\cdot\overline{BZ_1}}\right|\Rightarrow d_h(A',B')=d_h(A,B)$$

Suponha que a h-reta $\overline{AB}_h$, com pontos ideais $Z_1$ e $Z_2$, passa pelo h-ponto $O$ e, no plano $\mathbb{E}_\infty$, a reta $\overline{AB}$ passa pelo ponto $O_r$, ver Figura 14. Como $\alpha$ e $\beta_r$ são circunferências ortogonais, então $Z_1$ e $Z_2$ são inversos em relação à $\beta_r$, isso implica que no plano $\mathbb{H}$, os pontos ideais $Z_1$ e $Z_2$ são simétricos em relação a $r$. Assim, no $\mathbb{E}_\infty$, temos

$$\begin{equation}\label{eq.col1}\overline{O_rA}\cdot\overline{O_rA'}=\overline{O_rZ_1}\cdot\overline{O_rZ_2}\end{equation}$$

A partir da igualdade $\eqref{eq.col1}$ podemos ter as seguintes proporções, $\dfrac{\overline{O_rZ_1}}{\overline{O_rA}}=\dfrac{\overline{O_rA'}}{\overline{O_rZ_2}}$ ou $\dfrac{\overline{O_rZ_2}}{\overline{O_rA}}=\dfrac{\overline{O_rA'}}{\overline{O_rZ_1}}$. Aplicando a propriedade da proporção $\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a-b}{b}=\dfrac{c-d}{d}$, temos:

$$\begin{equation}\label{eq.col2}\left\{\begin{matrix}


\dfrac{\overline{O_rZ_1}}{\overline{O_rA}}=\dfrac{\overline{O_rA'}}{\overline{O_rZ_2}}\Rightarrow\dfrac{\overline{O_rZ_1}-\overline{O_rA}}{\overline{O_rA}}=\dfrac{\overline{O_rA'}-\overline{O_rZ_2}}{\overline{O_rZ_2}}\Rightarrow\dfrac{\overline{AZ_1}}{\overline{O_rA}}=\dfrac{\overline{A'Z_2}}{\overline{O_rZ_2}}\Rightarrow\overline{O_rA}=\dfrac{\overline{AZ_1}\cdot\overline{O_rZ_2}}{\overline{A'Z_2}}\\


\\


\dfrac{\overline{O_rZ_2}}{\overline{O_rA}}=\dfrac{\overline{O_rA'}}{\overline{O_rZ_1}}\Rightarrow\dfrac{\overline{O_rA}-\overline{O_rZ_2}}{\overline{O_rA}}=\dfrac{\overline{O_rZ_1}-\overline{O_rA'}}{\overline{O_rZ_1}}\Rightarrow\dfrac{\overline{AZ_2}}{\overline{O_rA}}=\dfrac{\overline{A'Z_1}}{\overline{O_rZ_1}}\Rightarrow\overline{O_rA}=\dfrac{\overline{AZ_2}\cdot\overline{O_rZ_1}}{\overline{A'Z_1}}


\end{matrix}\right.\end{equation}$$

De $\eqref{eq.col2}$ temos

$$\begin{equation}\label{eq.col3}


\dfrac{\overline{AZ_1}\cdot\overline{O_rZ_2}}{\overline{A'Z_2}}=\dfrac{\overline{AZ_2}\cdot\overline{O_rZ_1}}{\overline{A'Z_1}}\Rightarrow\dfrac{\overline{AZ_1}\cdot\overline{A'Z_1}}{\overline{AZ_2}\cdot\overline{A'Z_2}}=\dfrac{\overline{O_rZ_1}}{\overline{O_rZ_2}}


\end{equation}$$

Figura 14: Reta $\overline{AB}$ passa no ponto $O_r$

De forma análoga ao que foi feito em $\eqref{eq.col1},\eqref{eq.col2}$ e $\eqref{eq.col3}$, podemos chegar a

$$\begin{equation}\label{eq.col4}


\dfrac{\overline{BZ_1}\cdot\overline{B'Z_1}}{\overline{BZ_2}\cdot\overline{B'Z_2}}=\dfrac{\overline{O_rZ_1}}{\overline{O_rZ_2}}


\end{equation}$$

De $\eqref{eq.col3}$ e $\eqref{eq.col4}$ temos

$$\begin{equation}\label{eq.col5} \dfrac{\overline{AZ_1}\cdot\overline{A'Z_1}}{\overline{AZ_2}\cdot\overline{A'Z_2}}=\dfrac{\overline{BZ_1}\cdot\overline{B'Z_1}}{\overline{BZ_2}\cdot\overline{B'Z_2}}\Rightarrow\dfrac{\overline{AZ_1}\cdot\overline{BZ_2}}{\overline{AZ_2}\cdot\overline{BZ_2}}=\dfrac{\overline{A'Z_1}\cdot\overline{B'Z_1}}{\overline{A'Z_2}\cdot\overline{B'Z_2}}\end{equation}$$ $$\begin{equation}\label{eq.col6}\left|\ln\dfrac{\overline{AZ_1}\cdot\overline{BZ_2}}{\overline{AZ_2}\cdot\overline{BZ_2}}\right|=\left|\ln\dfrac{\overline{A'Z_1}\cdot\overline{B'Z_1}}{\overline{A'Z_2}\cdot\overline{B'Z_2}}\right|\Rightarrow d_h(A,B)=d_h(A',B') \end{equation}$$

$\square$

Teorema 1 - A reflexão em torno de uma h-reta é uma isometria.

DEMONSTRAÇÃO
As Proposições 1 e 2 garantem que a reflexão em torno de uma h-reta satisfazem  a Definição 1(a) e Definição 1(b). No plano $\mathbb{E}_\infty$, a reflexão em torno de uma reta é uma isometria, ou seja, é uma aplicação conforme (conserva ângulos), assim, no plano $\mathbb{H}$, se o h-eixo de simetria passa no ponto $O$, a reflexão em torno da h-reta conservará ângulos. Se o h-eixo de simetria não passa por $O$ a reflexão em torno da h-reta conservará ângulos, desta forma, a reflexão em torno de uma h-reta satisfaz a Definição 1(c).
$\square$
A seguir, a Construção 1 foi feita no Geogebra. Temos que $r$ é o h-eixo de simetria e determinada pelos h-pontos $P$ e $Q$; $s$ é uma h-reta determinada pelos h-pontos $A$ e $B$; $t$ é uma h-reta determinada pelos h-pontos $B$ e $C$, $Z_1$ e $Z_2$ são pontos ideais de $s$, $A',B',C',Z'_1$ e $Z'_2$ são os simétricos de $A,B,C,Z_1$ e $Z_2$, respectivamente.
Mova os h-pontos da cor amarela e observe a reflexão em torno da h-reta $r$. 

Construção 1: Reflexão em torno da h-reta $r$

ATUALIZADO EM 13/10/2017

Vamos considerar a definição a seguir para h-circunferências

Definição 3 - Dado um h-ponto $C$ e uma h-distância $\rho$, definiremos a circunferência hiperbólica $\lambda$, ou h-circunferência, com h-centro em $C$ e h-raio $\rho$ o conjunto dos h-pontos que estão a uma h-distância $\rho$ do h-ponto $C$.

Assim, podemos verificar que a reflexão em torno de uma h-reta transforma h-circunferências em h-circunferências com o mesmo h-raio.

Proposição 3 - Seja $\lambda$ uma h-circunferência com h-centro $C$ e h-raio $\rho$ e seja $\lambda'$ o simétrico de $\lambda$ em torno de uma h-reta $r$, então $\lambda'$ será uma h-circunferências com h-raio $\rho$.

DEMONSTRAÇÃO

Sendo $C'$ o simétrico de $C$ em torno de $r$, pelo Teorema 1, temos que $C'$ é um h-ponto que está a uma distância $\rho$ de qualquer h-ponto de $\lambda'$, assim, pela Definição 3, $\lambda'$ é uma h-circunferências com h-centro em $C'$ e h-raio $\rho$.

$\square$

Numa próxima postagem, veremos como é uma h-circunferência no modelo de Disco de Ponicaré.