Circunferências ortogonais
Através da construção de circunferências ortogonais, poderemos determinar h-retas e realizar transformações geométricas no h-plano. Veremos teoremas importantes que fundamentam a construção de uma circunferência ortogonal a uma circunferência dada.
Definição 1 - Considere duas circunferências, $C_1$ e $C_2$, que se intersetam em dois pontos, $A_1$ e $A_2$, no plano euclidiano. Sejam $r$ e $s$ retas que tangenciam, respectivamente, $C_1$ e $C_2$ no ponto $A_1$. O ângulo $\theta$ formado por $C_1$ e $C_2$ no ponto $A_1$ é o ângulo formado por $r$ e $s$ no ponto $A_1$. Se $\theta$ for $90^\circ$, dizemos que $C_1$ e $C_2$ são circunferências ortogonais.
Lema 1 - Sejam $C_1$ e $C_2$ circunferências que se intersetam nos pontos $A_1$ e $A_2$. O ângulo $\theta$ formado por $C_1$ e $C_2$ no ponto $A_1$ é congruente ao ângulo $\gamma$ formado por $C_1$ e $C_2$ no ponto $A_2$.
DEMONSTRAÇÃO
Considere as retas $r$ e $s$ tangentes, respectivamente, a $C_1$ e $C_2$ no ponto $A_1$, as retas $t$ e $u$ tangentes, respectivamente, a $C_1$ e $C_2$ no ponto $A_2$ e os pontos $E$, interseção entre $u$ e $s$, e $F$, interseção entre $r$ e $t$, ver Figura 3.
Definição 1 - Considere duas circunferências, $C_1$ e $C_2$, que se intersetam em dois pontos, $A_1$ e $A_2$, no plano euclidiano. Sejam $r$ e $s$ retas que tangenciam, respectivamente, $C_1$ e $C_2$ no ponto $A_1$. O ângulo $\theta$ formado por $C_1$ e $C_2$ no ponto $A_1$ é o ângulo formado por $r$ e $s$ no ponto $A_1$. Se $\theta$ for $90^\circ$, dizemos que $C_1$ e $C_2$ são circunferências ortogonais.
 |
| Figura 1: $\theta$ é o ângulo formado por $C_1$ e $C_2$ Se $\theta=90^\circ$ então $C_1$ é ortogonal a $C_2$ |
 |
| Figura 2: $\theta$ e $\gamma$ são congruentes |
DEMONSTRAÇÃO
Considere as retas $r$ e $s$ tangentes, respectivamente, a $C_1$ e $C_2$ no ponto $A_1$, as retas $t$ e $u$ tangentes, respectivamente, a $C_1$ e $C_2$ no ponto $A_2$ e os pontos $E$, interseção entre $u$ e $s$, e $F$, interseção entre $r$ e $t$, ver Figura 3.
 |
| Figura 3: Demonstração que $\theta$ e $\gamma$ são congruentes |
As retas $r$ e $s$ são tangentes a $C_1$ e se intersetam no ponto $F$, então $\overline{A_1F}=\overline{A_2F}$. De forma análoga, podemos mostrar que $\overline{A_1E}=\overline{A_2E}$. Assim, pelo caso Lado-Lado-Lado, os triângulo $\triangle_{A_1EF}$ e $\triangle_{A_2FE}$ são congruentes, logo, os ângulo $\theta$ e $\gamma$ são congruentes.
$\square$
Lema 2 - Considere a circunferência $C$ com centro num ponto arbitrário $O$ e raio $r\neq o$ e a reta $s$. A reta $s$ é ortogonal à circunferência $C$ se e somente se passar por $O$.
DEMONSTRAÇÃO
$\left.\Rightarrow\right)$ Considere os pontos $P$ e $Q$, interseções entre a reta $s$ e a circunferência $C$ , e a reta $t$, tangente a $C$ no ponto $P$. Se $s$ é ortogonal a $C$ então $s\perp t$. Vamos mostrar que a reta $s$ passa pelo ponto $O$, centro da circunferência $C$.
Considere que $s$ é secante a $C$ mas não passa por $O$, ver Figura 4. Assim, o ângulo central $\angle POQ$ é o dobro do ângulo formado pelas retas $s$ e $t$ no ponto $P$, ou seja, $\angle POQ = 180^\circ$. Assim, as semirretas $\overrightarrow{OP}$ e $\overrightarrow{OQ}$ estão na mesma reta, o que é absurdo. Logo, $s$ passa pelo ponto $O$.
$\left.\Leftarrow\right)$ Vamos considerar o ponto $P$, uma das interseções entre a reta $s$ e a circunferência $C$ e a reta $t$ tangente a $C$ no ponto $P$. Sendo $O$, centro da circunferência $C$, um dos pontos da reta $s$, vamos provar que $s\perp t$, assim, $s$ será ortogonal a $C$.
Vamos supor que $s$ e $t$ não sejam perpendiculares. Assim, existe um ponto $M\in t$ tal que $\overline{OM}\perp t$, por hipótese, os segmentos $\overline{OM}$ e $\overline{OP}$ não são coincidentes por que $\overline{OP}$ e $t$ não são perpendiculares. O ponto $M $ divide a reta $t$ em duas semirretas opostas. Vamos determinar na semirreta oposta a que tem o ponto $P$ o ponto $P'$ tal que $\overline{MP}\cong\overline{MP'}$ . Assim, os triângulo $\triangle_{OMP}$ e $\triangle_{OMP'}$ são congruentes, caso LAL, pois $\overline{OM}$ é o lado comum aos triângulos, $\overline{OM}$ é perpendicular a $t$ e $\overline{MP}\cong\overline{MP'}$, logo, $\overline{OP}\cong\overline{OP'}$, ver Figura 5, o que implica em $P'\in C$ que é absurdo, pois, por hipótese, a reta $t$ intercepta a circunferência $C$ apenas no ponto $P$. Portanto, a reta $s$ é ortogonal à circunferência $C$.
Lema 3 - Seja $P$ um ponto externo a uma circunferência $C$. Só há uma única circunferência ortogonal a $C$ com centro em $P$.
DEMONSTRAÇÃO
Digamos que existe uma circunferência ortogonal a $C$ que tem centro no ponto $P$, que denotaremos por $D$. Portanto, $D$ intercepta $C$ em dois pontos, $A$ e $B$. Pelo Corolário 1, a reta tangente a $C$ no ponto $A$ passa por $P$, assim como a reta tangente a $C$ no ponto $B$ também passa no ponto $P$. Como as retas $\overleftrightarrow{AP}$ e $\overleftrightarrow{BP}$ são tangentes a $C$, então $\overline{AP}\equiv\overline{BP}$ e não são nulos, pois $A$ e $B$ pertencem a circunferência $C$ e, por hipótese, $P$ é externo a $C$. Logo, a existência da circunferência $D$, ortogonal a $C$, com centro no ponto $P$ está condicionada a existência das retas $\overleftrightarrow{AP}$ e $\overleftrightarrow{BP}$ tangentes à circunferência $C$.
A construção abaixo foi feita no Geogebra e nos auxiliará na demonstração da existência das retas $\overleftrightarrow{AP}$ e $\overleftrightarrow{BP}$ tangentes a $C$ para todo ponto $P$ externo a $C$.
DEMONSTRAÇÃO
$\left.\Rightarrow\right)$ Considere os pontos $P$ e $Q$, interseções entre a reta $s$ e a circunferência $C$ , e a reta $t$, tangente a $C$ no ponto $P$. Se $s$ é ortogonal a $C$ então $s\perp t$. Vamos mostrar que a reta $s$ passa pelo ponto $O$, centro da circunferência $C$.
Considere que $s$ é secante a $C$ mas não passa por $O$, ver Figura 4. Assim, o ângulo central $\angle POQ$ é o dobro do ângulo formado pelas retas $s$ e $t$ no ponto $P$, ou seja, $\angle POQ = 180^\circ$. Assim, as semirretas $\overrightarrow{OP}$ e $\overrightarrow{OQ}$ estão na mesma reta, o que é absurdo. Logo, $s$ passa pelo ponto $O$.
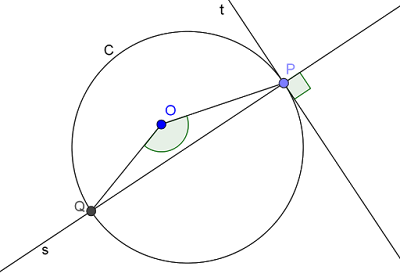 |
| Figura 4: Reta $s$ é ortogonal a circunferência $C$ |
Vamos supor que $s$ e $t$ não sejam perpendiculares. Assim, existe um ponto $M\in t$ tal que $\overline{OM}\perp t$, por hipótese, os segmentos $\overline{OM}$ e $\overline{OP}$ não são coincidentes por que $\overline{OP}$ e $t$ não são perpendiculares. O ponto $M $ divide a reta $t$ em duas semirretas opostas. Vamos determinar na semirreta oposta a que tem o ponto $P$ o ponto $P'$ tal que $\overline{MP}\cong\overline{MP'}$ . Assim, os triângulo $\triangle_{OMP}$ e $\triangle_{OMP'}$ são congruentes, caso LAL, pois $\overline{OM}$ é o lado comum aos triângulos, $\overline{OM}$ é perpendicular a $t$ e $\overline{MP}\cong\overline{MP'}$, logo, $\overline{OP}\cong\overline{OP'}$, ver Figura 5, o que implica em $P'\in C$ que é absurdo, pois, por hipótese, a reta $t$ intercepta a circunferência $C$ apenas no ponto $P$. Portanto, a reta $s$ é ortogonal à circunferência $C$.
 |
| Figura 5: reta $s$ passa pelo ponto $C$ |
$\square$
Como consequência do Lema 2, se duas circunferências, $C_1$ e $C_2$, são ortogonais no ponto $P$ e as retas $r$ e $s$ são tangentes, respectivamente, a $C_1$ e $C_2$ em $P$, então $r$ passa pelo centro de $C_2$ e $s$ passa pelo centro de $C_1$, ver Figura 6.
 - - |
| Figura 6: $r$ passa pelo centro $O_2$ de $C_2$ e $s$ passa pelo centro $O_1$ de $C_1$ |
Colorário 1 - Sejam $C_1$ e $C_2$ circunferências ortogonais que se intersetam no ponto $P$, $r$ é uma reta tangente a $C_1$ no ponto $P$ e $s$ é uma reta tangente a $C_2$ no ponto $P$. Então, $r$ incide no centro de $C_2$ e $s$ incide no centro de $C_1$.
DEMONSTRAÇÃO
Digamos que existe uma circunferência ortogonal a $C$ que tem centro no ponto $P$, que denotaremos por $D$. Portanto, $D$ intercepta $C$ em dois pontos, $A$ e $B$. Pelo Corolário 1, a reta tangente a $C$ no ponto $A$ passa por $P$, assim como a reta tangente a $C$ no ponto $B$ também passa no ponto $P$. Como as retas $\overleftrightarrow{AP}$ e $\overleftrightarrow{BP}$ são tangentes a $C$, então $\overline{AP}\equiv\overline{BP}$ e não são nulos, pois $A$ e $B$ pertencem a circunferência $C$ e, por hipótese, $P$ é externo a $C$. Logo, a existência da circunferência $D$, ortogonal a $C$, com centro no ponto $P$ está condicionada a existência das retas $\overleftrightarrow{AP}$ e $\overleftrightarrow{BP}$ tangentes à circunferência $C$.
A construção abaixo foi feita no Geogebra e nos auxiliará na demonstração da existência das retas $\overleftrightarrow{AP}$ e $\overleftrightarrow{BP}$ tangentes a $C$ para todo ponto $P$ externo a $C$.
1 - Marque o ponto médio $M$ entre $O$ e $P$;
2- Trace a circunferência $T$ com centro em $M$ e raio $\overline{MP}$ e marque os pontos $A$ e $B$, intercessão entre $C$ e $D$;
3- Trace as retas $\overleftrightarrow{AP}$ e $\overleftrightarrow{BP}$
4- Trace a circunferência $D$ com centro em $P$ e raio $\overline{AP}$.
A circunferência $D$ é ortogonal a $C$.
O ângulo $\angle OAP$ mede $90^\circ$, pois é o ângulo do arco capaz do diâmetro $\overline{OP}$ da circunferência $T$, como $\overline{OA}$ é raio da circunferência $C$, então $\overleftrightarrow{AP}$ é tangente a $C$. De forma análoga, provamos que $\overleftrightarrow{BP}$ é tangente a $C$. Assim, os pontos $A$ e $B$ só existirão se $P$ for um ponto externo a circunferência $C$. Logo, para todo $P$ externo à circunferência $C$ existe circunferência ortogonal a $C$ com centro no ponto $P$.
Vamos provar que a circunferência $D$ é única.
Suponhamos que existe uma ponto $A'$ distinto de $A$ e $B$ tal que a circunferência $T'$ com centro em $P$ e raio $\overline{A'P}$ é ortogonal à circunferência $C$. Então, o triângulo $\triangle_{OA'P}$ é retângulo em $A'$ e o ângulo $\angle OA'P$ é o ângulo do arco capaz do diâmetro $\overline{OP}$ da circunferência $T$, que é absurdo, pois $T$ interseta $C$ apenas em $A$ e $B$ que são distintos de $A'$. Logo, a circunferência $D$ é única.
3- Trace as retas $\overleftrightarrow{AP}$ e $\overleftrightarrow{BP}$
4- Trace a circunferência $D$ com centro em $P$ e raio $\overline{AP}$.
A circunferência $D$ é ortogonal a $C$.
O ângulo $\angle OAP$ mede $90^\circ$, pois é o ângulo do arco capaz do diâmetro $\overline{OP}$ da circunferência $T$, como $\overline{OA}$ é raio da circunferência $C$, então $\overleftrightarrow{AP}$ é tangente a $C$. De forma análoga, provamos que $\overleftrightarrow{BP}$ é tangente a $C$. Assim, os pontos $A$ e $B$ só existirão se $P$ for um ponto externo a circunferência $C$. Logo, para todo $P$ externo à circunferência $C$ existe circunferência ortogonal a $C$ com centro no ponto $P$.
Vamos provar que a circunferência $D$ é única.
Suponhamos que existe uma ponto $A'$ distinto de $A$ e $B$ tal que a circunferência $T'$ com centro em $P$ e raio $\overline{A'P}$ é ortogonal à circunferência $C$. Então, o triângulo $\triangle_{OA'P}$ é retângulo em $A'$ e o ângulo $\angle OA'P$ é o ângulo do arco capaz do diâmetro $\overline{OP}$ da circunferência $T$, que é absurdo, pois $T$ interseta $C$ apenas em $A$ e $B$ que são distintos de $A'$. Logo, a circunferência $D$ é única.
$\square$
Teorema 1 - Seja $C$ uma circunferência de centro $O$ e raio $r\neq 0$. Os pontos $P$ e $P'$ são inversos à circunferência $C$ se, e somente se, qualquer circunferência que passa por $P$ e $P'$ é ortogonal à circunferência $C$.
DEMONSTRAÇÃO
$\left.\Rightarrow\right)$ Na Figura 7, os pontos $P$ e $P'$ são inversos em relação a circunferência $C$ que tem centro no ponto $O$. $D$ é uma circunferência arbitrária que passa por $P$ e $P'$ e tem centro num ponto $Q$. O ponto $A$ é uma das interseções entre $C$ e $D$ e $M$ é o ponto médio do segmento $\overline{PP'}$. Para provar que $D$ é ortogonal a $C$ é necessário mostrar que as retas $\overleftrightarrow{OA}$ e $\overleftrightarrow{AQ}$ são perpendiculares, para isso basta provar que o triângulo $\triangle_{OAQ}$ é retângulo em $A$.
Como $P$ e $P'$ são pontos da circunferência $D$, então $\overline{QP}\equiv\overline{QP'}$, assim, o triângulo $\triangle_{PQP'}$ é isósceles. Sendo $M$ o ponto médio de $\overline{PP'}$, os segmento $\overline{PP'}$ e $\overline{QM}$ são perpendiculares. Portanto, o triângulo $\triangle_{OQM}$ é retângulo em $M$: $$\begin{equation}\label{OQM}\overline{OQ}^2=\overline{QM}^2+\overline{OM}^2\end{equation}$$
Temos ainda que $$\begin{equation}\overline{PP'}=\overline{MP}+\overline{MP'}=2\cdot\overline{MP}\end{equation}$$
$$\begin{equation}\label{MP} \overline{OP'}=\overline{OP}+\overline{PP'}=\overline{OP}+2\cdot\overline{MP} \Rightarrow
\overline{MP} =\dfrac{\overline{OP'}-\overline{OP}}{2} \end{equation}$$
$$\begin{equation} \label{OM}\overline{OM}=\overline{OP}+\overline{MP}=\overline{OP}+\dfrac{\overline{OP'}-\overline{OP}}{2}\Rightarrow\overline{OM}=\dfrac{\overline{OP'}+\overline{OP}}{2}\end{equation}$$
O triângulo $\triangle_{QMP}$ é retângulo em $M$, então $$\begin{equation}\label{QM}\overline{QP}^2=\overline{QM}^2+\overline{MP}^2\Rightarrow
\overline{QM}^2=\overline{QP}^2-\overline{MP}^2=\overline{QP}^2-\left( \dfrac{\overline{OP'}-\overline{OP}}{2} \right)^2\Rightarrow \\
\overline{QM}^2=\overline{QP}^2+\dfrac{2\cdot\overline{OP'}\cdot\overline{OP}-(\overline{OP'}+\overline{OP})}{4}\end{equation}$$
Fazendo $\eqref{OM}$ e $\eqref{QM}$ em $\eqref{OQM}$ temos
$$\begin{equation}\overline{OQ}^2=\overline{QP}^2+\dfrac{2\cdot\overline{OP'}\cdot\overline{OP}-(\overline{OP'}+\overline{OP})}{4}+\left(\dfrac{\overline{OP'}+\overline{OP}}{2}\right)^2= \\ \overline{QP}^2+\dfrac{2\cdot\overline{OP'}\cdot\overline{OP}-(\overline{OP'}+\overline{OP})}{4}+\dfrac{2\cdot\overline{OP'}\cdot\overline{OP}+(\overline{OP'}+\overline{OP})}{4}\end{equation}=\overline{QP}^2+\overline{OP'}\cdot\overline{OP}$$
Por hipótese, $P$ e $P'$ são inversos em relação a $C$ e $A$ é um ponto de $C$ e $D$, então
$$\begin{equation}\left\{\begin{array}{l}\overline{OP'}\cdot\overline{OP}=\overline{OA}^2 \\ \overline{QP}=\overline{QA}\end{array}\right.\end{equation}$$
Temos $$\overline{OQ}^2=\overline{QA}^2+\overline{OA}^2$$
Verificamos que o triângulo $\triangle_{OAQ}$ é retângulo em $A$, pois satisfaz o Teorema de Pitágoras.
$\left.\Leftarrow\right)$ Na Figura 8, $C$ e $D$ são circunferências ortogonais no ponto $A$. O ponto $O$ é o centro de $C$ e $h$ é um semirreta com origem em $O$ que intercepta $D$ nos pontos $P$ e $P'$.
Aplicando potência de ponto em relação à circunferência $D$, temos $$\overline{OP}\cdot\overline{OP'}=\overline{OA}^2$$ Como $\overline{OA}$ é raio da circunferência $C$, então $P$ e $P'$ são inversos em relação a $C$
DEMONSTRAÇÃO
$\left.\Rightarrow\right)$ Na Figura 7, os pontos $P$ e $P'$ são inversos em relação a circunferência $C$ que tem centro no ponto $O$. $D$ é uma circunferência arbitrária que passa por $P$ e $P'$ e tem centro num ponto $Q$. O ponto $A$ é uma das interseções entre $C$ e $D$ e $M$ é o ponto médio do segmento $\overline{PP'}$. Para provar que $D$ é ortogonal a $C$ é necessário mostrar que as retas $\overleftrightarrow{OA}$ e $\overleftrightarrow{AQ}$ são perpendiculares, para isso basta provar que o triângulo $\triangle_{OAQ}$ é retângulo em $A$.
 |
| Figura 7: Circunferência $D$ passa por $P$ e $P'$ e é ortogonal a $C$ |
Temos ainda que $$\begin{equation}\overline{PP'}=\overline{MP}+\overline{MP'}=2\cdot\overline{MP}\end{equation}$$
$$\begin{equation}\label{MP} \overline{OP'}=\overline{OP}+\overline{PP'}=\overline{OP}+2\cdot\overline{MP} \Rightarrow
\overline{MP} =\dfrac{\overline{OP'}-\overline{OP}}{2} \end{equation}$$
$$\begin{equation} \label{OM}\overline{OM}=\overline{OP}+\overline{MP}=\overline{OP}+\dfrac{\overline{OP'}-\overline{OP}}{2}\Rightarrow\overline{OM}=\dfrac{\overline{OP'}+\overline{OP}}{2}\end{equation}$$
O triângulo $\triangle_{QMP}$ é retângulo em $M$, então $$\begin{equation}\label{QM}\overline{QP}^2=\overline{QM}^2+\overline{MP}^2\Rightarrow
\overline{QM}^2=\overline{QP}^2-\overline{MP}^2=\overline{QP}^2-\left( \dfrac{\overline{OP'}-\overline{OP}}{2} \right)^2\Rightarrow \\
\overline{QM}^2=\overline{QP}^2+\dfrac{2\cdot\overline{OP'}\cdot\overline{OP}-(\overline{OP'}+\overline{OP})}{4}\end{equation}$$
Fazendo $\eqref{OM}$ e $\eqref{QM}$ em $\eqref{OQM}$ temos
$$\begin{equation}\overline{OQ}^2=\overline{QP}^2+\dfrac{2\cdot\overline{OP'}\cdot\overline{OP}-(\overline{OP'}+\overline{OP})}{4}+\left(\dfrac{\overline{OP'}+\overline{OP}}{2}\right)^2= \\ \overline{QP}^2+\dfrac{2\cdot\overline{OP'}\cdot\overline{OP}-(\overline{OP'}+\overline{OP})}{4}+\dfrac{2\cdot\overline{OP'}\cdot\overline{OP}+(\overline{OP'}+\overline{OP})}{4}\end{equation}=\overline{QP}^2+\overline{OP'}\cdot\overline{OP}$$
Por hipótese, $P$ e $P'$ são inversos em relação a $C$ e $A$ é um ponto de $C$ e $D$, então
$$\begin{equation}\left\{\begin{array}{l}\overline{OP'}\cdot\overline{OP}=\overline{OA}^2 \\ \overline{QP}=\overline{QA}\end{array}\right.\end{equation}$$
Temos $$\overline{OQ}^2=\overline{QA}^2+\overline{OA}^2$$
Verificamos que o triângulo $\triangle_{OAQ}$ é retângulo em $A$, pois satisfaz o Teorema de Pitágoras.
$\left.\Leftarrow\right)$ Na Figura 8, $C$ e $D$ são circunferências ortogonais no ponto $A$. O ponto $O$ é o centro de $C$ e $h$ é um semirreta com origem em $O$ que intercepta $D$ nos pontos $P$ e $P'$.
 |
| Figura 8: $C$ e $D$ são ortogonais no ponto $A$ |
$\square$
REFERÊNCIAS
KILHIAN, Kleber. Teorema do Ângulo Inscrito. 2011. Disponível em: <http://obaricentrodamente.
POTÊNCIA de ponto. 2012. Disponível em: <http://www.colegioweb.com.br/
SOUZA, Carlos Bino de. Geometria Hiperbólica: Consistência do Modelo de Disco de Poincaré. 2014. 114 f. Dissertação (Mestrado) - Curso de Mestrado Profissional em Matemática em Rede Nacional - Profmat, Ufrpe, Recife, 2014. Disponível em: <http://bit.profmat-sbm.org.


Comentários
Postar um comentário
Não postar comentários ofensivos e que contenham palavrões. Comente sobre o assunto da postagem que você leu.