Postagens
Mostrando postagens de 2016
Visualizações de página dos últimos 30 dias

Postado por
Carlos Bino
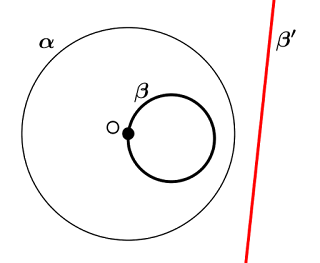
Inversão de ângulos formados por retas e circunferências
- Gerar link
- X
- Outros aplicativos
Postado por
Carlos Bino
Inversão de circunferência em relação a outra circunferência
- Gerar link
- X
- Outros aplicativos

Postado por
Carlos Bino
Inversão de reta em relação à circunferência
- Gerar link
- X
- Outros aplicativos

Postado por
Carlos Bino
GEOMETRIA HIPERBÓLICA: H-retas perpendiculares
- Gerar link
- X
- Outros aplicativos
Postado por
Carlos Bino
GEOMETRIA HIPERBÓLICA: Ângulo no h-plano
- Gerar link
- X
- Outros aplicativos
Postado por
Carlos Bino
GEOMETRIA HIPERBÓLICA: Construção de h-reta
- Gerar link
- X
- Outros aplicativos

Postado por
Carlos Bino
Circunferências ortogonais
- Gerar link
- X
- Outros aplicativos
Postado por
Carlos Bino
Inversão de um ponto qualquer do plano euclidiano em relação a uma circunferência
- Gerar link
- X
- Outros aplicativos
Postado por
Carlos Bino
Inversão de ponto externo a circunferência $\alpha$
- Gerar link
- X
- Outros aplicativos
Postado por
Carlos Bino
Inversão de ponto interno à circunferência $\alpha$
- Gerar link
- X
- Outros aplicativos
Postado por
Carlos Bino
Inversão na circunferência
- Gerar link
- X
- Outros aplicativos

Postado por
Carlos Bino
GEOMETRIA HIPERBÓLICA: Propriedades da Métrica do Disco de Poincaré
- Gerar link
- X
- Outros aplicativos
Mais visualizadas nos últimos 30 dias
Postado por
Carlos Bino
GEOMETRIA HIPERBÓLICA: Construção de h-reta
- Gerar link
- X
- Outros aplicativos

Postado por
Carlos Bino
GEOMETRIA HIPERBÓLICA: O modelo de Disco de Poincaré
- Gerar link
- X
- Outros aplicativos
