Pular para o conteúdo principal
Pesquisar
Pesquisar este blog
Bendita Matemática
Páginas
Curiosidades
Geometria Hiperbólica
Mais…
Postagens
Mostrando postagens de 2017
Mostrar tudo
Visualizações de página dos últimos 30 dias
Postado por
Carlos Bino
outubro 13, 2017
GEOMETRIA HIPERBÓLICA: Circunferência hiperbólica no Disco de Poincaré
Postado por
Carlos Bino
outubro 09, 2017
Aplicação da matemática para tomar uma decisão
Postado por
Carlos Bino
setembro 08, 2017
Elipse como sendo o lugar geométrico dos centros das circunferências tangentes a uma circunferência $d$, com centro $C$ e raio $r$, e que passa por um ponto $F\neq C$ interno à $d$
Postado por
Carlos Bino
julho 17, 2017
Utilizando uma circunferência para construir uma hipérbole
Postado por
Carlos Bino
julho 16, 2017
Associando pontos da circunferência a uma elipse ou hipérbole
Postado por
Carlos Bino
junho 29, 2017
Pontos equidistantes do centro e de algum lado de um quadrado
Postado por
Carlos Bino
fevereiro 28, 2017
5 TRUQUES MATEMÁTICOS QUE VÃO EXPLODIR SUA MENTE
Postado por
Carlos Bino
fevereiro 09, 2017
GEOMETRIA HIPERBÓLICA: Mediatriz e H-ponto médio no Disco de Poincaré
Postado por
Carlos Bino
janeiro 28, 2017
GEOMETRIA HIPERBÓLICA: H-eixo de simetria no Disco de Poincaré
Postado por
Carlos Bino
janeiro 24, 2017
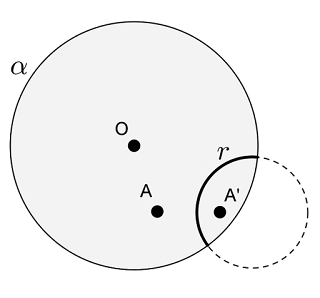
GEOMETRIA HIPERBÓLICA: Isometria no Disco de Poincaré - Reflexão em torno de uma h-reta
Postado por
Carlos Bino
janeiro 13, 2017
Arco triplo
Postado por
Carlos Bino
janeiro 08, 2017
Centro do inverso de uma circunferência que não passa pelo centro de inversão
Postagens mais recentes
Postagens mais antigas
Página inicial
Mais visualizadas nos últimos 30 dias
Postado por
Carlos Bino
janeiro 13, 2017
Arco triplo
Postado por
Carlos Bino
junho 29, 2017
Pontos equidistantes do centro e de algum lado de um quadrado
Postado por
Carlos Bino
março 05, 2021
Assíntota oblíqua
